The circle of fifths is an incredible tool that has many different uses when it comes to music theory. It can help us with everything from knowing what chord progressions will sound good together to what sharps or flats a key signature has.
In this post, I’m going to give you an overview of this useful musical concept and explain some of the ways that it can help you learn music theory.
What Is The Circle Of Fifths?

As the name implies, the circle of fifths is a circle that connects all 12 tones used in Western music. It is a visual representation of the musical relationship between these 12 tones.
By using the circle of fifths, you can quickly and easily determine the key signature of any major or minor key and the chords that will sound good together in a given key.
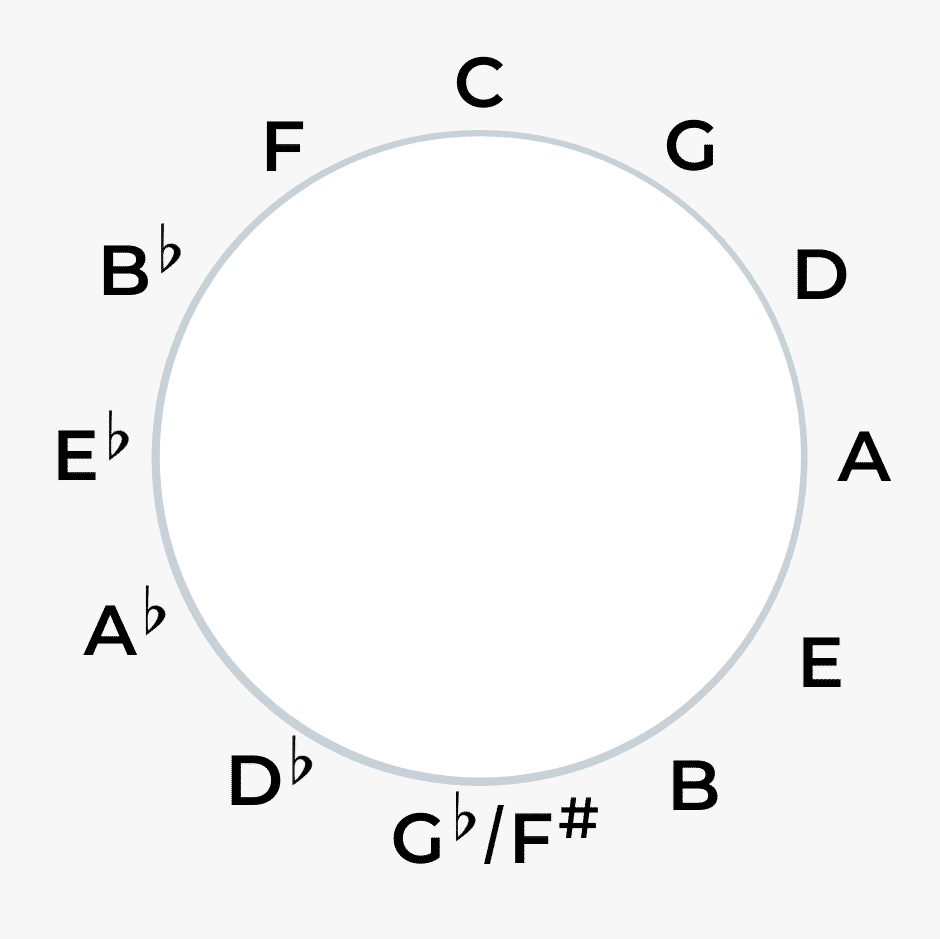
This makes it an essential tool for anyone learning music theory or for musicians who want to better understand the underlying structure of the music they play.
Building The Circle
To build the circle of fifths, we place all 12 note letter names around a circle like a clock.
But rather than putting them in order from A to G, each of the notes is separated by intervals of perfect fifths.
We start with the note C at the top of the circle (where 12 would be on a clock face).
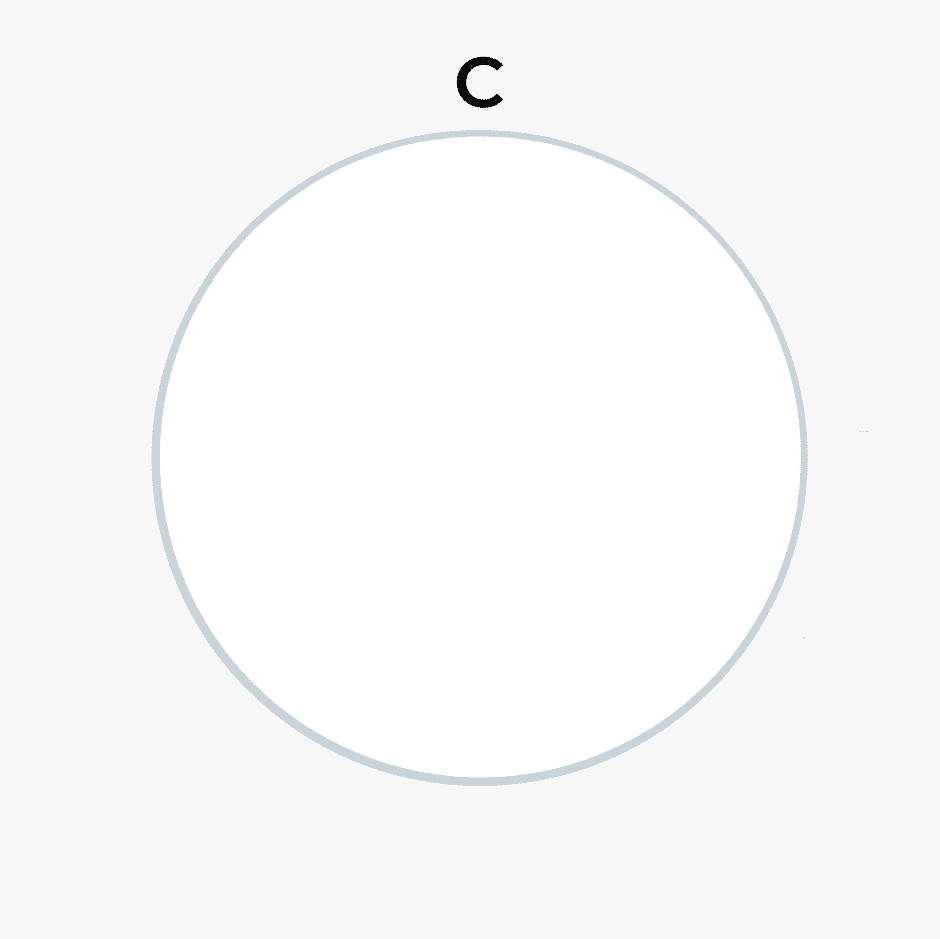
We then add the next note in the circle by adding a note to the right of C (where one would be on a clock face) that is an interval of a perfect fifth above C.
Going up a perfect fifth from C, we reach G, and we carry on clockwise around the circle, adding the note a perfect 5th above.
Up a perfect fifth from G, we reach D, then A, then E, then B, then F#.
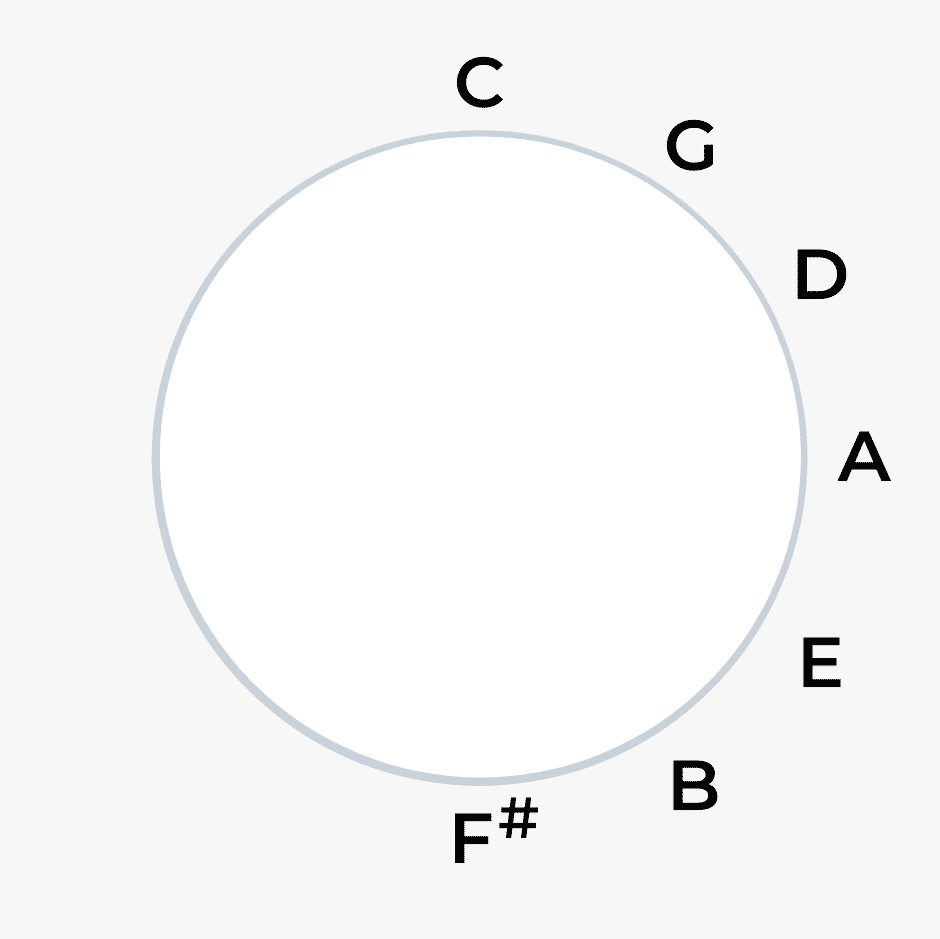
We could carry on going up perfect fifths from F# to C# and then C# to G#, but there is an easier way.
We can go back to the C at the top in the middle and this time go down a perfect fifth and write notes to the left of C.
To work out what note is a perfect fifth below C, we can go down seven semitones (half steps).
Seven semitones down from C is F, so we can add the note F next to C (11 on a clock face).
We can then continue adding each note a perfect fifth below the previous note.
A perfect fifth below F is Bb, Bb to Eb, Eb to Ab, Ab to Db, and finally from Db to Gb.
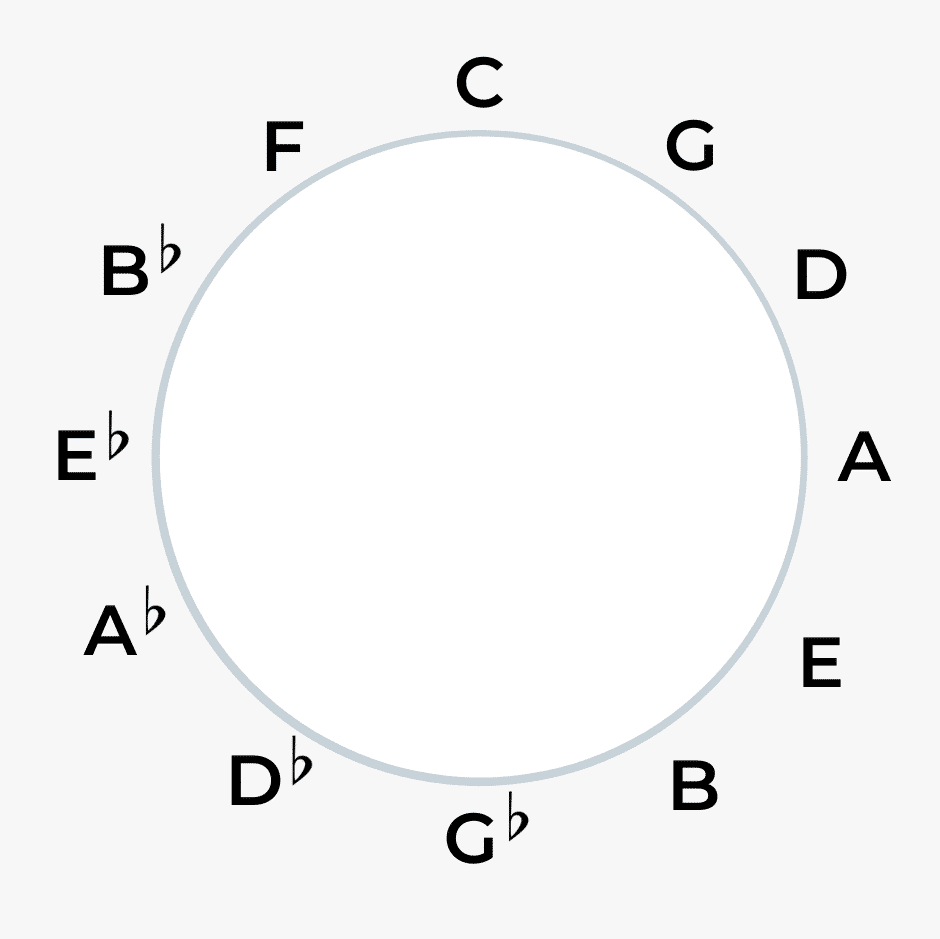
Side note:
F# and Gb are what we call enharmonic equivalents, which is just a fancy way of saying they’re the same but with different names. So you’ll often see both notes at the bottom of the circle of fifths.
How To Memorize The Circle Of Fifths
Now that we’ve built a circle, we have to remember it rather than just memorize it through sheer repetition. We can do this in a few ways.
The best way is through a mnemonic device — we create a sentence with the first letter of each word starting with a new note in the circle.
For example, Charles Goes Dancing At Every Big Fun Celebration.
The first letter of every word (C – G – D – A – E – B – F – C) follows the circle of fifths, starting at the top C and going right (the last two notes here are technically F# and C#, remember).
This also represents the order of key signatures that have sharps (#) in them — C has no sharps, G has 1 sharp, D has 2, etc., all the way to C#, which has seven sharps.
Starting at C and going the other way (to the left), we have the mnemonic example: Charles Falls Behind Everyone At Disc Golf Courses.
Going this way, we have the notes C, F, Bb, Eb, Ab, Db, Gb, and Cb, which are also in order of how many flats they have in their key signatures: C has none, F has one flat, Bb has two, … and Cb has seven flats.
However, as shown in the picture above, some of these keys are enharmonic equivalents: Cb = B, Gb = F#, and Db = C#.
This is something to look out for when memorizing the mnemonic sentences.
How To Use The Circle Of Fifths
The circle of fifths has several very handy uses. Now I’ll cover a few things we can use it for.
Working Out Key Signatures
Just like we noticed in the two sentences above, the farther you go down on the right side of the circle, the more sharps you have in a key, and the farther you go down on the left side, the more flats you have.
The top of the circle has no flats or sharps — C major.
Going down the right side, you gain one sharp to your key signature every note for the first seven notes (you can only have at max seven sharps or flats in any key signature).
Going down the left side, you gain one flat to your key signature for the first seven notes.
Working Out The Relative Major And Minor Keys
If you’re in any key, you can use the circle of fifths to figure out the relative major or minor of that key.
If you start in a major key, to find the relative minor key, you go to the right three spaces in the circle.
For example, if your key is C major, you go right three spaces (C – G – D – A) to get A, so the relative minor of C major is A minor.
If you’re in E major, your relative minor is C# minor; if you’re in Ab major, your relative minor is F minor.
And vice versa, if you’re in a minor key and want to find out the relative major, just go to the left three spaces.
For example, C minor to the left for three spaces (C – F – Bb – Eb) is Eb major.
If you’re in B minor, the relative major is D major; the relative major for Ab minor is Cb major.
See if you can write out the relative major and minor of each key.
Chords To Use In A Song
These days, most modern pop songs tend to use four chords to make their harmonies and melodies. These four chords are easy to find on the circle of fifths.
In a major key, you start with the key that you’re in (for example, A major). Then, you also use the relative minor (three spaces to the right).
In A major, this would be F# minor. Then, you add the keys on either side of your main key (one space to the right and left).
So in A major, you would then get D major and E major. And there are your four chords: A major, D major, E major, and F# minor.
In C major, your four chords for a song are C major, F major, G major, and A minor.
You’ll now be able to play a lot of different songs. This video by the comedy musical act Axis of Awesome demonstrates how great these four chords are. (Warning: contains some bad language).
Try figuring out the pop chords for all the other keys!
Other Interesting Uses
There are some other interesting ways we can use the circle of fifths.
For example, if you move two spaces to the right, you have stepped up one whole tone. For example, from C, two to the right gets you D, which is a whole tone above C.
From this, you can make the whole tone scale — just go two spaces to the right each time: C – (skip G) – D – (skip A) – E – F# – Ab – Bb – C.
Another cool feature is you can figure out what a tritone interval is for each note.
A tritone is six semitones (half steps) away from a note.
To figure this out using the circle of fifths, just take any note (e.g., Db) and go directly opposite that note on the circle (or move over six spaces).
The note opposite Db is G, so G-Db is a tritone interval.
The C at the top of the circle is opposite the F#/Gb at the bottom of the circle, so C-F# is a tritone.
Summing Up
That’s all for the circle of fifths!
There is a lot of cool stuff to learn and understand about its uses, so take your time, write it out yourself on a piece of paper, and see all the interesting relationships between the notes and chords for yourself.
This is one of the most fundamental and helpful tools in all of music theory, and it basically defines harmonic progressions for most contemporary music like pop, rock, and jazz.
We hope you were able to learn something about the circle of fifths.



